突然ですがみなさん、錐の体積の求め方はご存知ですか?
体積=底面積×高さ×1/3
ですよね。こちらは中学1年生で習う公式です。
教科書でこの公式を知ったとき、授業でこの公式を習ったとき、
1/3はなんで1/3なんだろうか
そんな風に思いませんでしたか?
この記事ではこの1/3の理由を説明します。
読み終わったときみなさんには、どや顔で友達に説明できるようになるでしょう。
錐の体積の公式の求め方
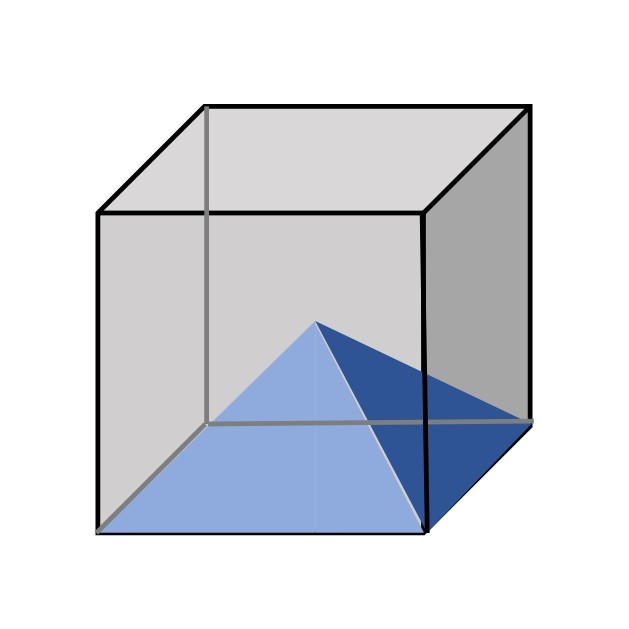
① 立方体を用意する。
そのまんまです。1辺がaの立方体を書いてみましょう。
1辺がaなので、この立方体の体積は、
a×a×a=a3
ですね。
下の図をイメージしてください。
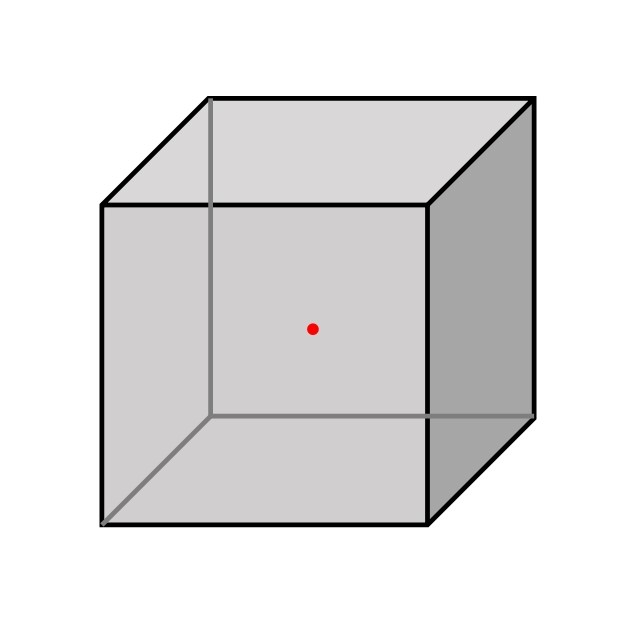
② 中心に点を打つ。
立方体のちょうど真ん中に中心の点を打ちましょう。
言葉で説明すると、上下の正方形の中心を結んだ線と、向かい合う側面の正方形の中心を結んだ線の交わるところです。
こちらも図を用意しました。
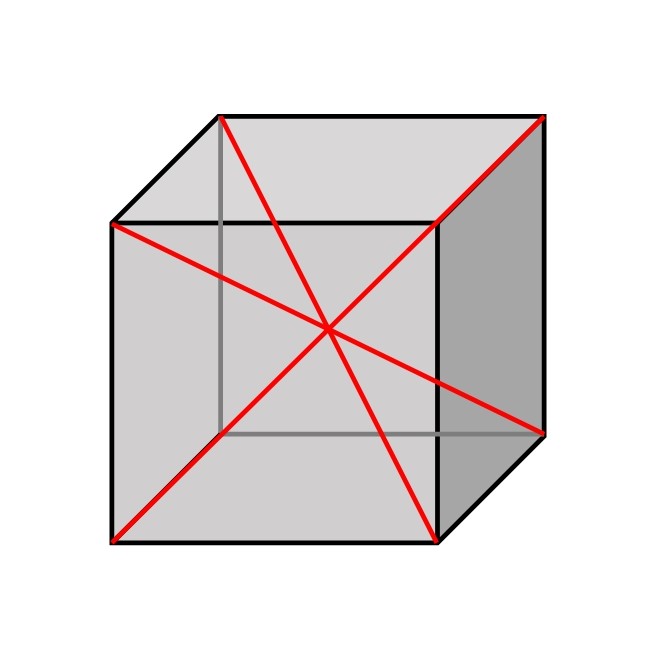
③ 中心の点から線を引く。
次は②で用意した点から各頂点に線を引いていきます。
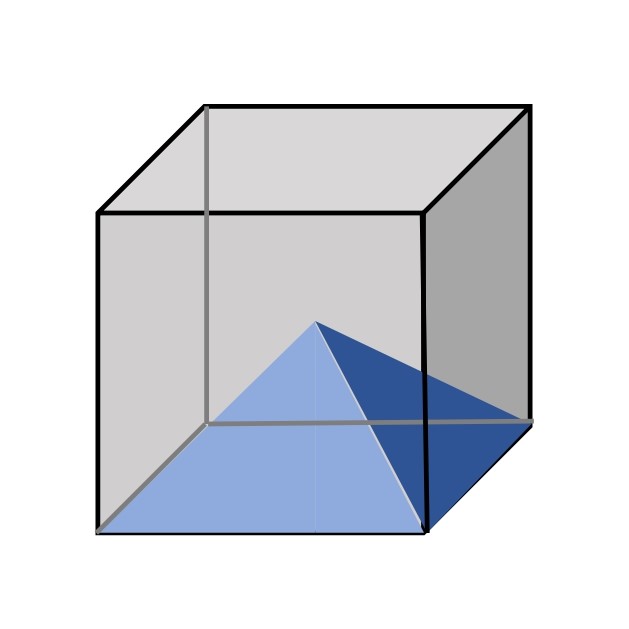
すると、全く同じ形をした四角錐が上下・左右・手前奥の計6つ見つかります。
④ 四角錐の体積は?
ここで、立方体の体積を思い出しましょう。
一辺がaなので、体積はa3でした。
さて、全く同じ形の四角錐6つが立方体に綺麗に収まっていますね。
したがって四角錐1つの体積は、
a3×1/6
⑤ 公式を作ろう。
では次は公式化してみましょう。
今考えていた四角錐の底面は1辺がaの正方形なので、底面積は、
a×a=a2
ですね。
次に高さは、立方体の半分の高さとなっているので、
a×1/2
です。
したがって、底面積と高さを使って公式をつくるためには、
a2×a×1/2×x=a3×1/6
とならなくてはいけません。
このxについての方程式を解くと、
x=1/3
が出てきます。これが錐の体積を求める公式に登場する1/3の正体です。
今求めた四角錐の体積との比をとることで、他の一般的な錐の体積も求めることができます。
他の錐の体積の公式
さて、では他の錐にも拡張してみましょう。
一辺がaの立方体の体積はa3、1つの四角錐の底面積はa2、高さはa×1/2、体積はa3×1/6でしたね。
底面積が半径aの円である円錐を横に並べて、ふたつの立体図形を見比べてみましょう。
このふたつの底面積の比は、
a2:πa2=1:π
ですね。
高さが同じところで、それぞれの錐を切ってみます。
すると、ふたつの錐の底面積の比は、常に1:πになることがわかります。
よって、体積の比も常に1:πになります。
そして、求めたい円錐の体積は、さっき体積を求めた四角錐と高さが同じa/2であることに注目すると、
a3×1/6×π/1=πa3×a×1/2×1/3=πa3×1/6
となります。公式通りですね。
ちなみに…。
今説明した内容は、中学生範囲で完結しています。
しかし、高校数学で学習する「積分」という考え方でも、錐の体積を求めることができます。
とてもざっくりいうと、
非常に薄い紙を何枚も何枚も重ねると立体的な形を作ることができる
という考え方です。
具体的な計算方法は高校数学の数学Ⅲで学習しますので、ぜひ高校での学習を楽しみにしていてください。
まとめ
いかがだったでしょうか。
今回の記事のポイントは、
・体積の公式は立方体の体積から考える!
・比を使って他の形にも応用可能!
・高校の「積分」でも公式は作れる!
ということでした!
どうでしょう、公式に関してすっきりできましたか?
ぜひこの考え方をマスターして、友達をぎゃふんといわせましょう!