
~数学オリンピック2024予選第3問~難易度★
問題
問題はこちらのリンクをクリックして見てください。数学オリンピック財団のHPに飛びます。
数オリの問題です。第3問から脱落者が少し増えてくるかもしれません。一番初めの図形問題で図も書いているので,本選に進むなら確実に正解しておきたいところです。
まずは,実際に解いてみて,できなかったら解説を読んで,理解できなかったところを重点的に復習しましょう。
解答
答え:$5+\sqrt{10}$
思考とプロセス
数オリの予選の図形は
チェバの定理・メネラウスの定理を利用する問題
と
方べきの定理の逆・円周核の定理の逆などを利用して円を見つけ,その円をもとに図形を展開していく問題
のおよそ2つに分けられると思います。今回は図形も書いていますし,円なので,方べきの定理等を活用していきましょう。
図のように,$BX=x, BD=y$とおきます。
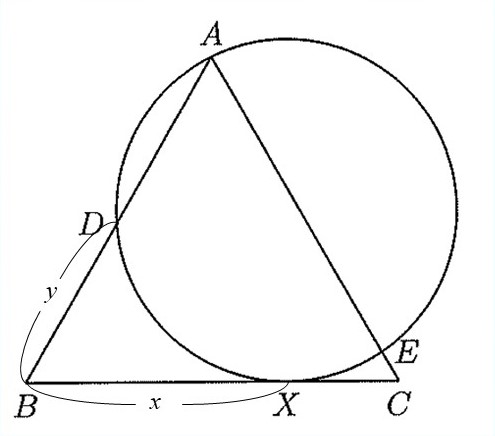
$\triangle{ABC}$は1辺が10の正三角形だったので,$AD=10-y, CX=10-x$ということも分かります。
さらに,$AD+AE=16$という条件から,$AE=16-AD=16-(10-y)=6+y$ということがわかり,$CE=10-AE=10-(6+y)=4-y$ということも分かります。
さらに,方べきの定理から,
$BD \cdot BA=BX^2$
$CE \cdot CA=CX^2$
ということもわかるので,
$10y=x^2$
$10(4-y)=(10-x)^2$
となるので,辺々を加えることにより,
$40=2x^2-20x+100$
という2次方程式ができます。これを解くと,$x=5 \pm \sqrt{10}$となりますが,$BX>CX$より,$BX>5$でないといけないので,$BX=5+\sqrt{10}$と求めることができます。