はじめに
中学数学の関数の分野では、変化の割合という用語が登場します。「変化の割合って何?どうやって計算するの?」と問われた時に、みなさんは正しく答えられますか?また、傾きや比例定数との違いも説明できるでしょうか?
変化の割合について理解し、似た用語である傾き、比例定数との違いまで押さえることで、関数分野の問題をスピーディーに解答できるようになります。また、3年生で学習する「$y=ax^2$ (二次関数)」の単元ではこれらについて十分に分かっていないと誤った答えになってしまうような問題もあります。
しかし、多くの子がこれらについて曖昧な理解のまま勉強を進めているのではないかと思います。
そこで、この記事では関数分野の変化の割合について解説し、傾きや比例定数との違いについても、直線(一次関数)と曲線(二次関数)にわけて解説していきます。また、二次関数の変化の割合を求める裏ワザについても紹介します。
目次
- 変化の割合とは
- 変化の割合、傾き、比例定数の違い
-
- 直線($y=ax、y=ax+b$)の場合
- 曲線($y=ax^2$)の場合
- 変化の割合の裏ワザ
変化の割合とは
変化の割合とは、「$x$が増えた時に$y$がどれくらい増えるか」を表した値です。
式で表現すると、 $変化の割合=\displaystyle\frac{yが増えた量}{xが増えた量}$ となります。
この式から分かる通り、変化の割合は「$x$が1増えた時に$y$がいくつ増えるかを表す値」「$x$が増えた量に対する、$y$が増える量の割合」とも言い換えることができます。
例:$y=2x+1$について、$x$の値が$3$から$7$まで増加するときの変化の割合を求めよ。
$x$の増えた量、$y$の増えた量をそれぞれ求めて、最後に分数にして答えを出します。
$x$の値は$3$から$7$まで増えているので、$x$の増えた量は$4$です。
一方で、$y$の値は$x=3$のとき$7、x=7$のとき$15$なので、$7$から$15$までで$y$の増えた量は8です。
最後に変化の割合の式に当てはめると、$\displaystyle\frac{yが増えた量}{xが増えた量}=\frac{8}{4}=2$
となります。
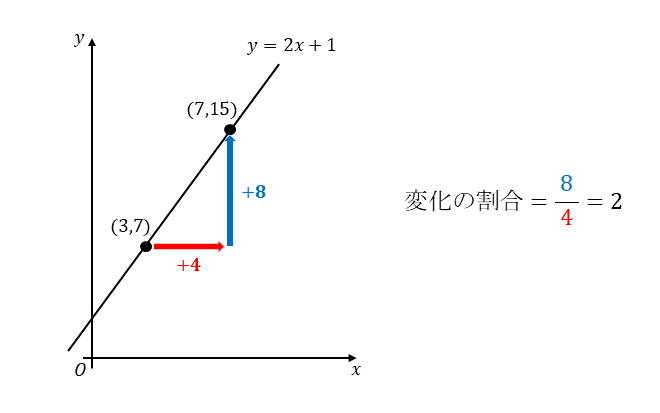
これをグラフで表現するとこのようになります。
$x$が$3$の点から$7$の点までで、$x$と$y$それぞれの増えた量は$4$と$8$。したがって、求める答えは$\displaystyle\frac{8}{4}=2$。
このように、$x$と$y$がそれぞれいくつ増えたのかに注目し、その比を分数で表せば変化の割合を求めることができます。
変化の割合、傾き、比例定数の違い
では次に、変化の割合、傾き、比例定数の3つの違いについて見てみましょう。
まずは傾きと比例定数について思い出しておきましょう。
傾き
傾きは1年生で習う比例($y=ax$)と2年生で習う一次関数($y=ax+b$)で登場する用語です。
両者に共通するのは式をグラフにしたときにどちらも直線であるということ。傾きは直線に対して使われる用語です。日常生活でも、「あの坂は傾きが急だなー」などと言うと思います。その傾きとおよそ同じです。
傾き=直線がどれくらい傾いているかを表す値
と思っておけばよいでしょう。
傾きがプラスの場合はその直線は右上がりであり、反対に傾きがマイナスの場合はその直線は右下がりであるとわかります。
直線の傾きは、式のある部分を見れば一発で誰でもわかります。それは、$y=ax、y=ax+b$の$a$です。学校でも必ず習います。「直線の傾きは$a$」と覚えておきましょう。
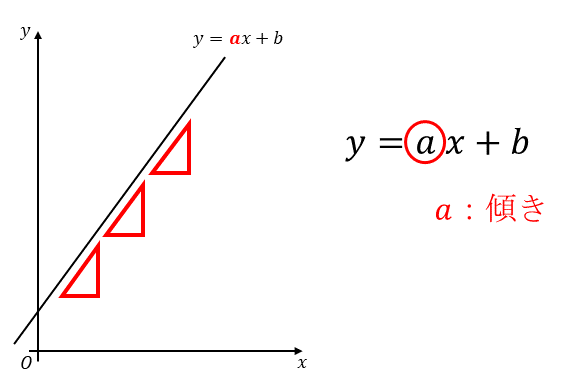
比例定数
比例定数は1年生で習う比例・反比例($y=ax、y=a\dfrac{1}{x}$)と3年生で習う二次関数($y=ax^2$)で登場する用語です。2年生の一次関数では出てきません。
比例定数は$y=ax、y=a\displaystyle\frac{1}{x}、y=ax^2$における$a$です。単純ですね。みなさんは「比例定数は$a$だ!」と覚えてしまってokです。しかし、中には「比例定数が$a$なのは分かったけど、そもそも比例定数って何?どういう意味?」と気になる子もいるでしょう。
そうした子のために、軽く説明を加えておきます。中学数学において比例定数は「△と⚪︎が△=$a$×⚪︎と表せるとき、$a$を比例定数と呼ぶ。」となっています。△と⚪︎には比例であれば$y$と$x$が、反比例であれば$y$と$\displaystyle\frac{1}{x}$が、二次関数であれば$y$と$x^2$が当てはまります。一次関数($y=ax+b$)は式が△=$a$×⚪︎というようにはなっていないので、比例定数はなしということになるわけです。

さて、それでは変化の割合、傾き、比例定数について、直線(比例、一次関数)と曲線(二次関数)にわけてみてみます。
直線($y=ax、y=ax+b$)の場合
結論から言えば、直線の場合の変化の割合、傾き、比例定数の値はどれも同じです。必ず同じなので、変化の割合をわざわざ計算する必要はありません。学校でもそう習ったのではないでしょうか。
先ほどの例で考えてみると、$y=2x+1$で$x$が$3$から$7$まで増えるときの変化の割合は$2$でした。この直線の式の傾きは、先の傾きの説明の通り$y=ax+b$の$a$の部分を見ればよいので$2$です。比例定数は一次関数なので存在しません。
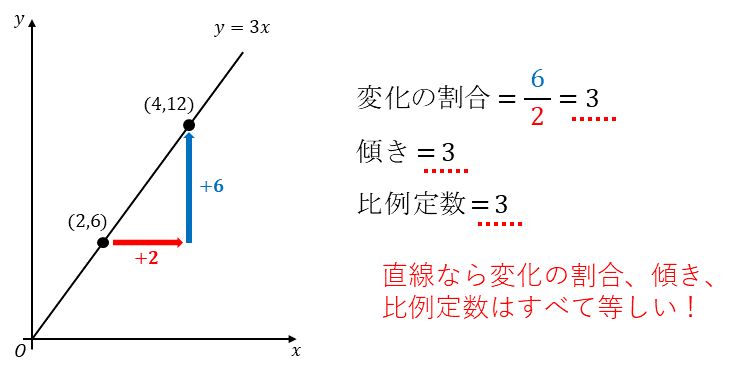
同じように、例えば$y=3x$で$x$が$2$から$4$まで増える場合では変化の割合を計算すると、$\displaystyle\frac{6}{2}=3$となります。傾きは$3$です。比例定数も$3$です。
以上のように、直線においては変化の割合、傾き、比例定数は同じであり、その値は$y=ax、y=ax+b$の$a$となります。
さらに、ここから言えるもう一つ重要なこととして「$x$の区間により変化の割合が変化しない」ということがあります。冒頭で、変化の割合は「$x$が増えた時に$y$がどれくらい増えるか」を表した値だと説明しました。これを踏まえて以下の図をみてみると、直線においては$x$がどの値であっても、その増える量が同じであれば$y$の増える量は同じであることがわかります。
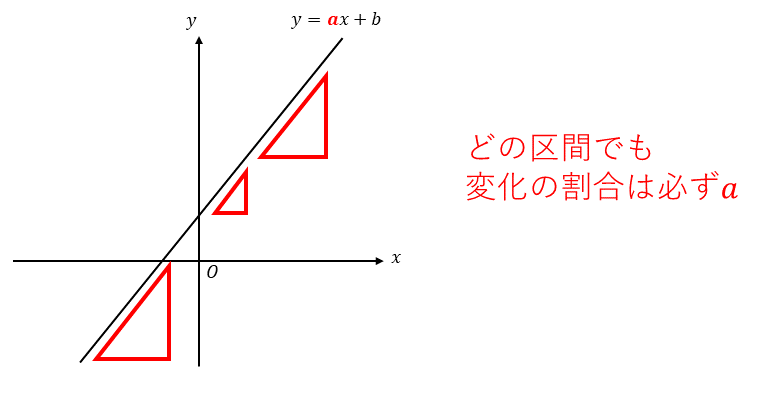
「直線では変化の割合も傾きも比例定数も全部$a$になる」と覚えておきましょう。
曲線($y=ax^2$)の場合
直線では変化の割合、傾き、比例定数の値は全て同じでしたが、残念ながら二次関数の場合はそうはいきません。一つずつみてみましょう。
まず、変化の割合は決まり通り計算する必要があります。$変化の割合=\displaystyle\frac{yが増えた量}{xが増えた量}$にしたがって、計算で求めましょう。
次に、二次関数には傾きは存在しません。それは中学数学において傾きは直線にのみ使われる用語だからです。
最後に、二次関数における比例定数は$y=ax^2$の$a$です。これは上でも説明した通り、「△と⚪︎が△=$a$×⚪︎と表せるとき、$a$を比例定数と呼ぶ。」ということを当てはめればokです。
以上のように、二次関数では変化の割合は計算の必要があり、傾きは存在せず、比例定数は$a$となります。それぞれで違うことを理解してください。
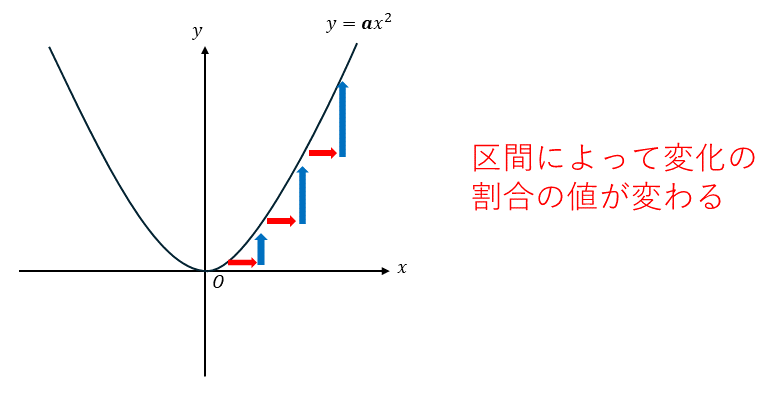
また、二次関数の変化の割合で注意してほしいこととして、「$x$の区間により変化の割合の値が変わる」ということがあります。先ほど、直線においては$x$がどの値であっても増える量が同じなら$y$の増える量も同じであり、その結果変化の割合も常に一定になると説明しましたが、二次関数ではそうはなりません。$x$が大きくなるほど$y$の「増え方」も大きくなるという二次関数の性質により、変化の割合の値は$x$の区間によって変化します。

以上のことを踏まえて、直線と曲線ごとに変化の割合、傾き、比例定数について表にまとめると以下のようになります。

これらの違いに基づく問題は定期テストではよく出ますし、高校入試でも出題されることがあります。しっかりと覚えておきましょう。
変化の割合の裏ワザ
ここまで読んだみなさんは「二次関数の変化の割合をいちいち式通りに計算するのがめんどくさい」と感じているかもしれません。実際に、$変化の割合=\displaystyle\frac{yが増えた量}{xが増えた量}$にしたがって計算すると、$y$が増えた量を求めるために$x$の値を二次関数の式に代入する作業が2回必要で、非常に煩わしく感じられます。
そこで、二次関数の変化の割合を一瞬で求めるための裏ワザをご紹介します。
裏ワザ
$y=ax^2$が$x=p$から$x=q$まで変化するときの変化の割合は、$a(p+q)$である。
実に簡単です。比例定数$a$に、$x$の変化前と変化後を足し算した数をかければおしまい。定義通りに計算するのがバカバカしくなってきます。実際の例で確認しましょう。
例:$y=3x^2$が$x=2$から$5$まで変化するときの変化の割合
$a=3、p=2、q=5$なので、$3\times(2+5)=21$
一瞬で求められました。この裏ワザは$a、p、q$がどんな値であっても成り立つので、時短テクニックとして覚えておき、定期テストなどでフル活用することをお勧めします。
ちなみに、なぜこの裏ワザが成り立つのかについては、変化の割合の式通りに$y=ax^2$が$x=p$から$x=q$まで変化するときの変化の割合を計算することで簡単に証明することができます。
変化の割合の式通りに考えると、$x$の増えた量は$q-p$、$y$の増えた量は$aq^2-ap^2$です。これらを用いて計算を進めると以下のように分母と分子の$q-p$が約分され、$a(p+q)$だけが残ることがわかります。
$変化の割合=\displaystyle\frac{aq^2-ap^2}{q-p}=\frac{a(q+p)(q-p)}{q-p}=a(q+p)$
まとめ
この記事では、変化の割合の基本的な説明から、傾きや比例定数との違い、変化の割合を求める裏ワザまで解説しました。学校でも1、2、3年生のそれぞれで変化の割合について学習しますが、こうして学年横断的に捉え直すと、頭の中が綺麗にまとまり、スッキリするはずです。また、裏ワザを用いることで煩わしい計算も回避できます。
この記事を読んだみなさんが変化の割合への抵抗がなくなり、二次関数が少しでも得意になってくれることを期待しています。